线性代数
向量
向量(vector):也可以叫做矢量。它代表一组数字,并且这些数字是有序排列的
C++中的数组就叫做vector
向量可以用来表示某个物体的特征。其中,向量的每个元素就代表一维特征,而元素的值代表了相应特征的值,我们称这类向量为特征向量
向量空间
x1,x2,……,xn∈F,就有 Fn
假设 V 是 Fn 的非零子集,如果对任意的向量 x、向量 y∈V,都有 (x+y)∈V,我们称为 V 对向量的加法封闭;对任意的标量 k∈V,向量 x∈V,都有 kx 属于 V,我们称 V 对标量与向量的乘法封闭
如果 V 满足向量的加法和乘法封闭性,我们就称 V 是 F 上的向量空间
向量子空间
已知 V:=(V,+,⋅) 是一个向量空间,如果 U⊆V,U !=0 ,那么 U:=(U,+,⋅) 就是 V 的向量子空间
距离
可以把一个向量想象为 n 维空间中的一个点。而向量空间中两个向量的距离,就是这两个向量所对应的点之间的距离
- 曼哈顿距离
$$MD(x,y) = \sum_{i=1}^n |x_i - y_i|$$
- 欧氏距离
$$ED(x,y) = \sqrt{\sum_{i=1}^n (x_i - y_i)^{2}}$$
- 切比雪夫距离
$$CD(x,y) = \argmax_1^n |x_i - y_i|$$
长度
通常使用欧氏距离来表示向量的长度
夹角
空间中两个向量所形成夹角的余弦值
$$Cosine(X,Y) = \frac{\sum_{i=1}^n (x_i * y_i)}{ \sqrt{\sum_{i=1}^n x^2 * \sum_{i=1}^n y^2}}$$
向量空间模型
向量空间模型假设所有的对象都可以转化为向量,然后使用向量间的距离,或者是向量间的夹角余弦来表示两个对象之间的相似程度
向量空间可以很形象地表示数据点之间的相似程度,不仅能运用在信息检索,也可以运用在基于相似度的一些机器学习算法中,例如 K 近邻(KNN)分类、K 均值(K-Means)聚类
信息检索:
- 将文档转为特征向量,分词后将词转换为向量,最简单的方法是用“1”表示这个词条出现在文档中,“0”表示没有出现,也可以对不同的词赋予不同的权重来丰富特征
- 将查询和文档进行匹配,查询需要先转为向量,因为查询与文档的维度不一样(出现的词),对于在文档出现而在查询没有出现的词,可以采取简单的置0,或者把文档的这个维度剔除掉
- 进行上面两个步骤后,就能得到每篇文档与查询的相似度了
线性无关
一组向量被称为线性无关,如果其中没有一个向量可以表示为其他向量的线性组合。换句话说,如果不存在非零标量使得这些向量的线性组合等于零向量,那么这些向量就被称为线性无关
$$ a_1\mathbf{v}_1+a_2\mathbf{v}_2+\cdots+a_n\mathbf{v}_n=\mathbf{0} $$
如果只有所有系数都为零的情况下,能够使得上述线性组合等于零向量,那么这组向量就是线性无关的
基与秩
一个向量空间的基(Basis)是一组线性无关的向量,它们可以表示该向量空间中的任何向量,并且这组向量是极小的——移除其中任何一个向量都会导致表示能力丧失,基是向量空间中的一个生成集,它使得空间中的每个向量都可以通过线性组合得到,且这个表示方式是唯一的
矩阵的秩表示矩阵中线性无关的列向量或者行向量的最大数量
- 列秩(Column Rank): 一个矩阵的列秩是它的列向量组成的向量空间的维度。也就是说,它是矩阵中线性无关的列向量的最大数量。列秩等于这个矩阵的列空间的维度
- 行秩(Row Rank): 一个矩阵的行秩是它的行向量组成的向量空间的维度。行秩等于矩阵的列秩
线性映射
描述了两个向量空间之间的关系,将一个向量空间的元素映射到另一个向量空间中
线性映射是一种函数,它满足以下两个性质:
- 加法性质 对于任意两个向量 $u$ 和 $v$,有 $f(u+v) = f(u) + f(v)$
- 数乘性质 对于任意标量 $c$ 和向量 $v$,有 $f(cv) = c \cdot f(v)$
可以用变换矩阵来描述这种映射,已知两个向量空间 V 和 W,它们各自相应的有序基是 B=(b1,⋯,b3) 和 C=(c1,⋯,c4) ,线性映射 ϕ 表示成以下形式
$$ \begin{aligned} &\phi\left(b_{1}\right) =c_1-c_2+3c_3-c_4 \ &\phi\left(b_{2}\right) =2c_1+c_2+7c_3+2c_4 \ &\phi\left(b_{3}\right) =3c_2+c_3+4c_4 \end{aligned} $$
其变换矩阵为
$$ \left.A_\phi=\left[\begin{array}{ccc}1&2&0\-1&1&3\3&7&1\-1&2&4\end{array}\right.\right] $$
- 核空间:关注的是向量空间 V 中所有经过 ϕ 映射为零的向量集合
- 像空间:向量空间 V 中所有经过 ϕ 映射后的向量集合
仿射空间
$V$ 是一个向量空间,$U$ 是 $V$ 的一个向量子空间,$x_0$ 是 $V$ 中的元素,那仿射子空间 $L$ 就等于:$L=x_0+U := {x_0+u:u\in U}$
$U$ 叫做方向,$x_0$ 叫做支撑点
- 一维仿射子空间,也叫做“线”,参数方程是:$y=x_0+λb_1$
- 二维仿射子空间,也叫做“平面”,参数方程是:$y=x_0+λ_1b_1+λ_2b_2$
- n−1 维仿射子空间,也叫做“超平面” $y=x_0+\sum_{i=1}^{n-1}\lambda_ib_i$
每个 V 到 W 的仿射映射,都是“一个 V 到 W 的线性映射”和“一个 W 到 W 平移”的组合
统一,仿射映射也可以用仿射变换矩阵表示
$$ \left.A'=\left[\begin{array}{cccc}1&0&0&x\0&1&0&y\0&0&1&z\0&0&0&1\end{array}\right.\right] $$
以上表示的就是一个针对 x y z 三个点平移对应距离的矩阵
运算
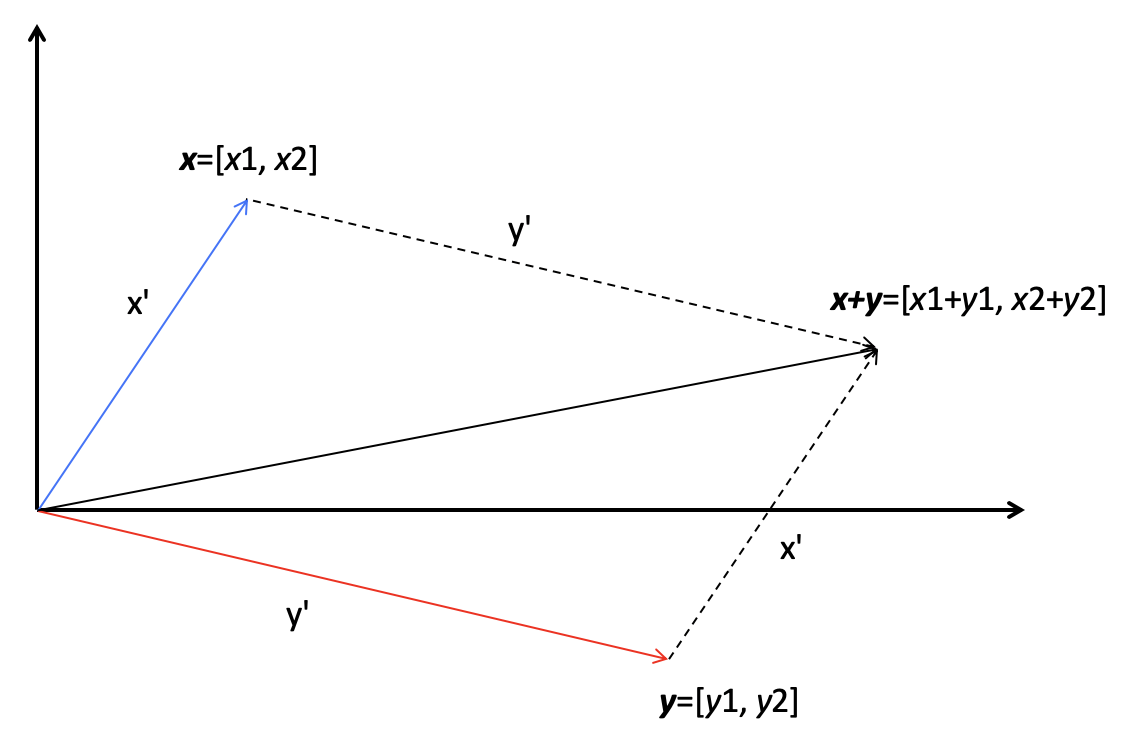
- 向量相加
$$ x=\begin{bmatrix}x_1\x_2\x_3\\varvdots\x_n\end{bmatrix}\quad y=\begin{bmatrix}y_1\y_2\y_3\\varvdots\y_n\end{bmatrix}\quad x+y=\begin{bmatrix}x_1+y_1\x_2+y_2\x_3+y_3\\varvdots\x_n+y_n\end{bmatrix} $$
- 向量相乘
$$ xy=\begin{bmatrix}x_1\x_2\x_3\\vdots\x_n\end{bmatrix}\begin{bmatrix}y_1\y_2\y_3\\vdots\y_n\end{bmatrix}=x_1y_1+x_2y_2+x_3y_3+...+x_ny_n $$
矩阵
矩阵由多个长度相等的向量组成,其中的每列或者每行就是一个向量
使用矩阵表示方程
$$ \left.\left{\begin{array}{c}a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n=b_1\a_{21}x_1+a_{22}x_2+\cdots+a_{2n}x_n=b_2\\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\a_{m1}x_1+a_{m2}x_2+\cdots+a_{mn}x_n=b_m\end{array}\right.\right. $$
=
$$ \left.\tilde{A}=\left[\begin{array}{ccccc}a_{11}&a_{12}&\ldots&a_{1n}&b_1\a_{21}&a_{22}&\ldots&a_{2n}&b_2\\ldots&\ldots&\ldots&\ldots&\ldots\a_{m1}&a_{m2}&\ldots&a_{mn}&b_m\end{array}\right.\right] $$
矩阵运算
矩阵相加
$$ A\in\mathbb{R}^{m\times n}, B\in\mathbb{R}^{m\times n} $$
$$ \left.A+B=\left[\begin{array}{ccc}a_{11}+b_{11}&\ldots&a_{1n}+b_{1n}\\cdot&&\cdot\\cdot&&\cdot\\cdot&&\cdot\a_{m1}+b_{m1}&\ldots&a_{mn}+b_{mn}\end{array}\right.\right]\in R^{m\times n} $$
矩阵乘
- 普通矩阵乘
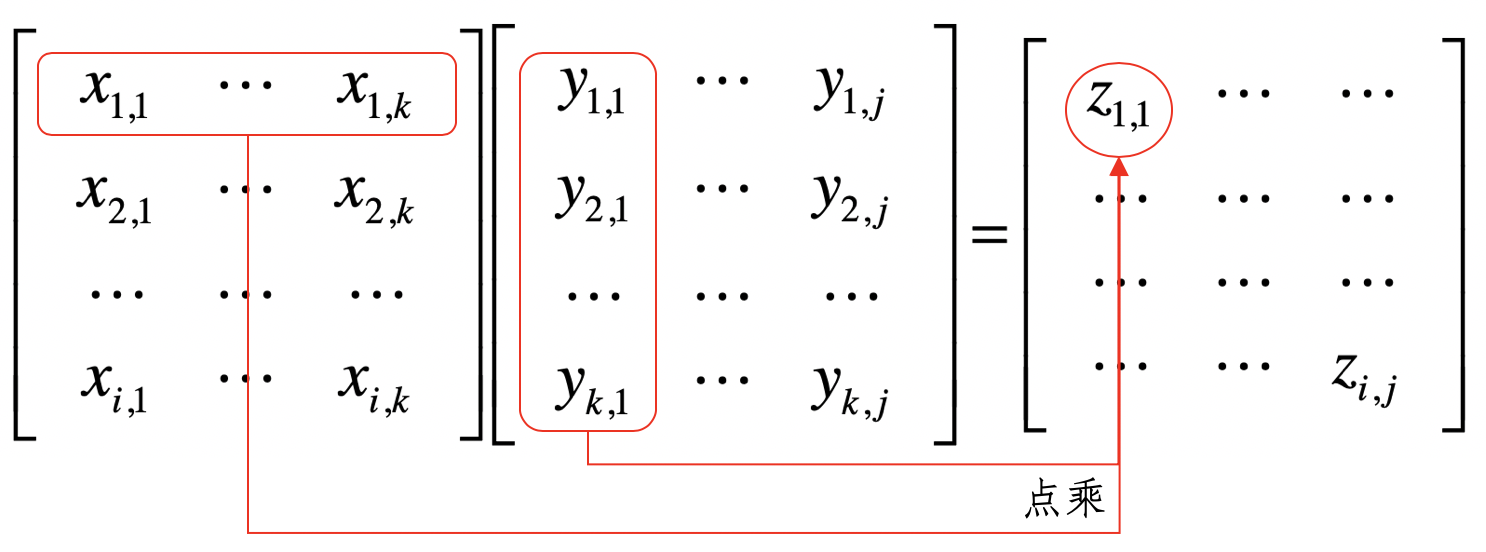
只有相邻阶数匹配的矩阵才能相乘,例如,一个 n×k 矩阵 A 和一个 k×m 矩阵 B 相乘,最后得出 n×m 矩阵 C,而这里的 k 就是相邻阶数
- 哈达玛积,就是矩阵各对应元素的乘积
$$ \left.C=A^B=\left[\begin{array}{cc}1&2\4&5\end{array}\right.\right]\left[\begin{array}{cc}1&4\2&5\end{array}\right]=\left[\begin{array}{cc}11&24\42&5*5\end{array}\right]=\left[\begin{array}{cc}1&8\8&25\end{array}\right] $$
- 克罗内克积,是两个任意大小矩阵间的运算
A×B,如果 A 是一个 m×n 的矩阵,而 B 是一个 p×q 的矩阵,克罗内克积则是一个 mp×nq 的矩阵
单位矩阵
主对角线上的元素均为 1,除此以外全都为 0
$$ \left.I_1=[1],I_2=\left[\begin{array}{ccc}1&0\0&1\end{array}\right.\right],I_3=\left[\begin{array}{ccc}1&0&0\0&1&0\0&0&1\end{array}\right],\ldots,I_n=\left[\begin{array}{cccc}1&0&\ldots&0\0&1&\ldots&0\.&.&\ldots&.\.&.&.&.\0&0&\ldots&1\end{array}\right] $$
矩阵的性质
- 结合律:任意实数 m×n 矩阵 A,n×p 矩阵 B,p×q 矩阵 C 之间相乘,满足结合律 (AB)C=A(BC)
- 分配律:任意实数 m×n 矩阵 A 和 B,n×p 矩阵 C 和 D 之间相乘满足分配律 (A+B)C=AC+BC,A(C+D)=AC+AD
- 单位矩阵相乘:任意实数 m×n 矩阵 A 和单位矩阵之间的乘,等于它本身 A
逆矩阵
A 乘以它的逆矩阵 $A^{-1}$ 就等于单位矩阵.如果一个矩阵是可逆的,那这个矩阵我们叫做非奇异矩阵,如果一个矩阵是不可逆的,那这个矩阵我们就叫做奇异矩阵
矩阵转置
$$ \left.x=\left[\begin{array}{cccc}x_{1,1}&x_{1,2}&x_{1,3}&x_{1,4}\x_{2,1}&x_{2,2}&x_{2,3}&x_{2,4}\x_{3,1}&x_{3,2}&x_{3,3}&x_{3,4}\\end{array}\right.\right] $$
$$ \left.x'=\left[\begin{array}{ccc}x_{1,1}&x_{2,1}&x_{3,1}\x_{1,2}&x_{2,2}&x_{3,2}\x_{1,3}&x_{2,3}&x_{3,3}\x_{1,4}&x_{2,4}&x_{3,4}\end{array}\right.\right] $$
线性回归
- 当自变量 x 的个数大于 1 时就是多元回归
- 当因变量 y 个数大于 1 时就是多重回归
如果因变量和自变量为线性关系时,就是线性回归模型;如果因变量和自变量为非线性关系时,就是非线性回归分析模型
高斯消元
主要分为两步,消元(Forward Elimination)和回代(Back Substitution)
设如下方程矩阵表达:
$$ \left.\left[\begin{array}{cccccc}1&-2&1&-1&1&|&0\4&-8&3&-3&1&|&2\-2&4&-2&-1&4&|&-3\1&-2&0&-3&4&|&a\end{array}\right.\right] $$
以第一行为基础,开始执行乘和加变换,将第一行乘以 -4 的结果和第二行相加,再将第一行乘以 2 的结果,再和第三行相加,不断消元
$$ \left.\left[\begin{array}{cccccc|c}1&-2&1&-1&1&|&0\0&0&1&-1&3&|&-2\0&0&0&1&-2&|&1\0&0&0&0&0&|&a+1\end{array}\right.\right] $$
得出 a 为 -1时,方程有解
通过程式之间的运算,消除未知的x
最小二乘法
解未知参数,使得理论值与观测值之差(即误差,或者说残差)的平方和达到最小
PCA主成分分析
一种针对数值型特征、较为通用的降维方法
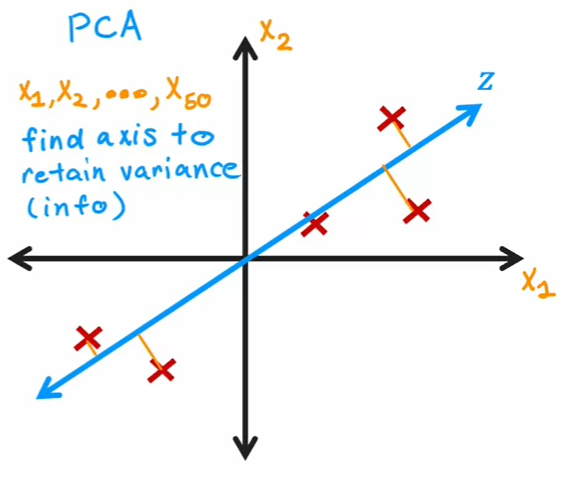
- 标准化样本矩阵中的原始数据;
- 获取标准化数据的协方差矩阵;
- 计算协方差矩阵的特征值和特征向量;
- 依照特征值的大小,挑选主要的特征向量;
- 生成新的特征
主成分每个轴之间都会成九十度
SVD 奇异值分解
通过样本矩阵本身的分解,找到一些“潜在的因素”,然后通过把原始的特征维度映射到较少的潜在因素之上,达到降维的目的